2번 문제는 여인수 전개로 determinant를 구하는 문제였습니다.

위에 정의된 행렬 $M$을 작성해보면 다음과 같습니다.
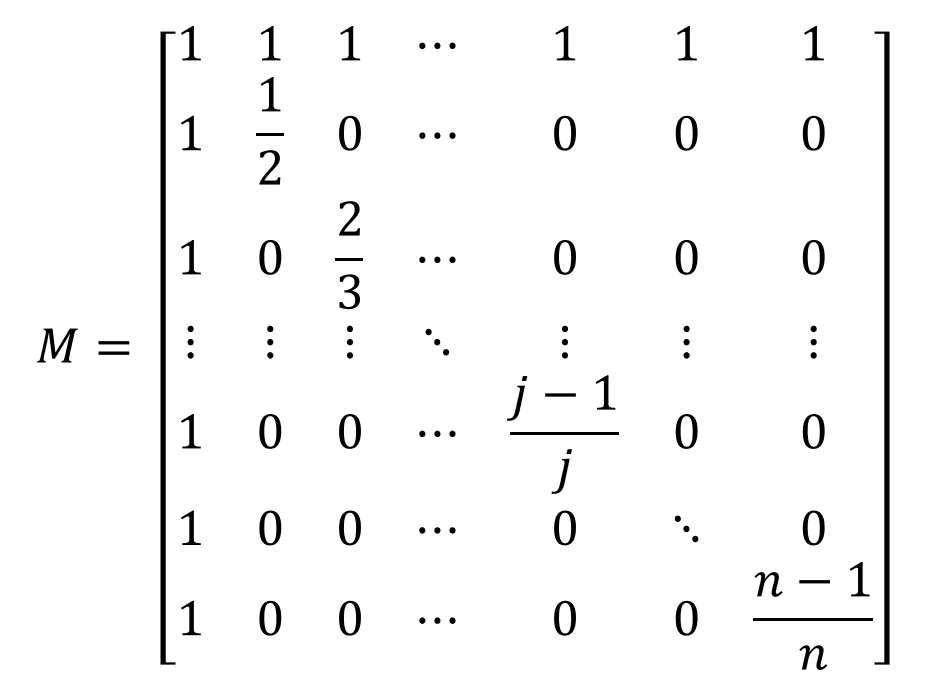
여기에서 $\det(M)$을 $n$으로 표현하는 것이 문제에서 원하는 답입니다. 그리고 구하고자 하는 것이 $n\det(M)+1+\frac{1}{2} + \cdots + \frac{1}{n-1}$이므로 점화식 또는 수열을 떠올려보는 것도 좋을 것 같습니다.
문제 풀이를 하기 전에 여인수 전개에 대해 먼저 작성해보겠습니다.
- 여인수 전개
3by3 행렬 $A$를 다음과 같이 정의해봅시다.

$M_{ij}$는 $a_{ij}$의 소행렬식, $C_{ij}$는 $a_{ij}$의 여인수라고 하면
소행렬식 $M_{ij}$는 $a_{ij}$를 기준으로 $i$행과 ${j}$열을 제외한 나머지 행렬을 의미하고
여인수 $C_{ij}$는 $(-1)^{(i+j)}M_{ij}$를 의미합니다.
여기서 $\det(A) = a_{11}C_{11} + a_{12}C_{12} + a_{13}C_{13}$로 나타내집니다.
위의 전개는 1행에 의한 전개이고 어느 행 또는 열을 기준으로 전개해도 determinant값은 동일하게 나옵니다. ㅅ
따라서 0이 많이 포함된 행 또는 열을 기준으로 여인수 전개를 하면 쉽게 determinant값을 얻을 수 있습니다.
예시를 들어 소행렬식을 구해보겠습니다.
$M_11$은 $a_11$의 소행렬식으로 행렬$A$에서 1행과 1열을 제외한 행렬의 determinant로 다음과 같이 정의됩니다.

이제 여인수 전개를 이용하여 위의 2번 문제를 해결해보도록 하겠습니다.
우선 어떤 행 또는 열을 기준으로 여인수 전개를 할 지를 고민해봐야 합니다. 저는 연산이 가장 편해보이는 $n$번째 열을 선택했습니다. 다른 열을 기준으로 해도 계산은 되겠지만 복잡해 보입니다.
$n$번째 열에는 0을 제외한 원소가 $1$행과 $n$행에 각각 $1, \frac{n-1}{n}$이 존재합니다.
따라서 $M_{1n}, M_{nn}$을 구하면 $C_{1n}, C_{nn}$또한 구할 수 있고 determinant값을 구할 수 있습니다.
목표 : $C_{1n}$과 $C_{nn}$을 구해서 $det(M) = a_{1n}C_{1n} + a_{nn}C_{nn}$ 을 구하려 한다.
따라서 $C_{1n}$과 $C_{nn}$을 구하는 것이 목표
- $M_{1n}$
$M_{1n}$을 구하기 위한 소행렬을 구해보면 $M$에서 $1$행 $n$열을 제외한 행렬입니다.

위의 표시된 행과 열을 제외한 소행렬의 determinant $M_{1n}$은 다음과 같습니다.
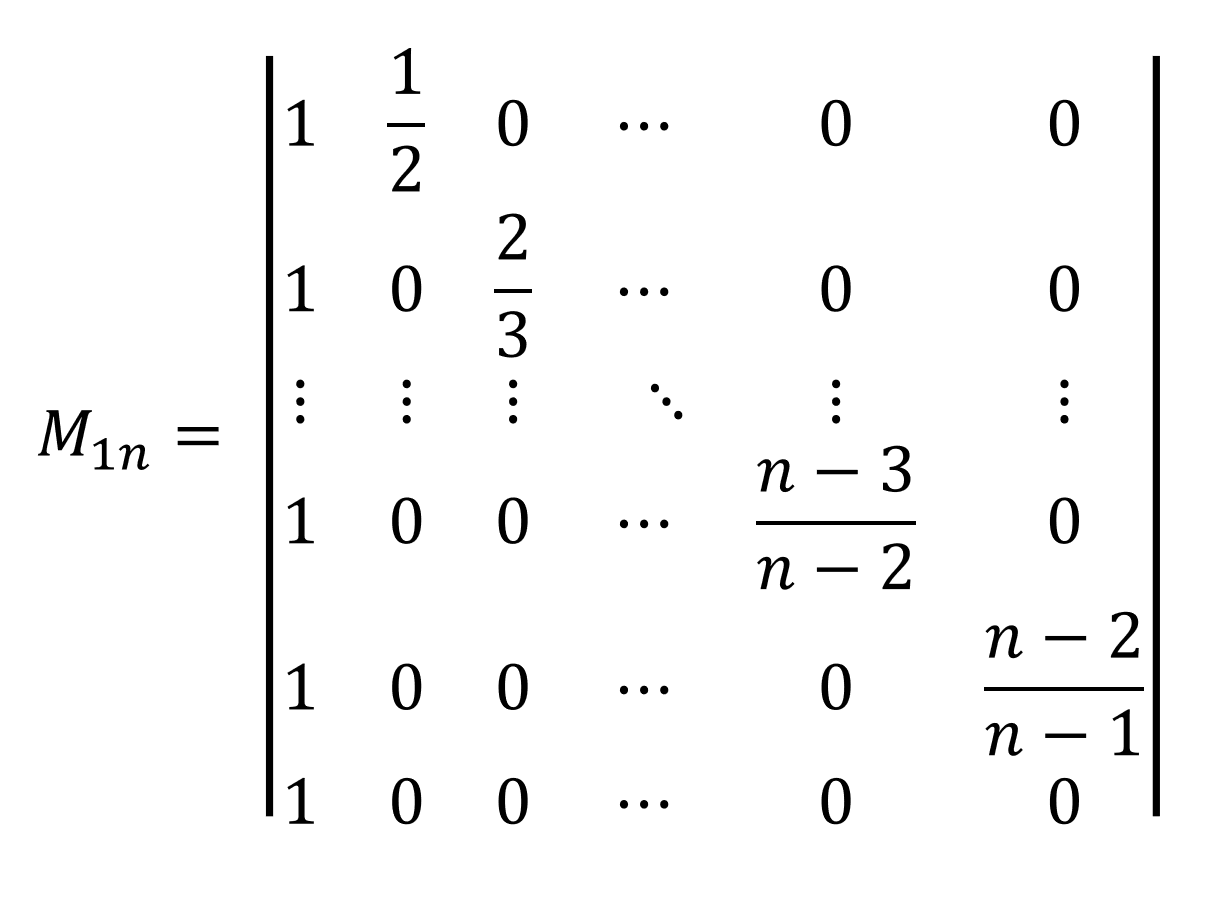
위의 $M_{1n}$에서 $i$번째 행을 $i+1$번째 행에 빼는 연산을 하면 상삼각행렬이 되는 것을 어렵지 않게 확인하실 수 있을 것입니다.
기본 행연산은 determinant값을 변화시키지 않기 때문에 determinant값을 구하기 쉬운 상삼각행렬로 기본 행연산을 통해 행렬을 변형해서 행렬식을 구하는 과정입니다.
$i$번째 행을 $i+1$번째 행에 빼서 determinant를 구하면
$M_{1n} = 1\times (-\frac{1}{2}) \times (-\frac{2}{3}) \times \cdots \times (-\frac{n-1}{n-1}) = (-1)^{n-2}\frac{1}{n-1}$ 입니다.
$M_{1n}$에 대한 여인수 $C_{1n}$을 구해보면
$C_{1n} = (-1)^{n+1} \times M_{1n} = (-1)^{2n-1}\frac{1}{n-1} = -\frac{1}{n-1}$입니다.
이제 $det(M) = a_{1n}C_{1n} + a_{nn}C_{nn}$ 에서 $a_{1n}C_{1n}$은 해결했고 $a_{nn}C_{nn}$을 해결할 차례입니다.

'[수학] > [대학생 수학 경시대회]' 카테고리의 다른 글
| [대수경] 제 39회 대학생 수학 경시대회 2분야 문제 1. (0) | 2021.08.08 |
|---|